CSci 301 Lecture Notes

Week Three, Tuesday: Context-Free Grammars

A context-free grammar is a collection of substitution rules (productions) defining how variables yield (produce) strings of variables and terminals. These substitution rules (that replace variables) are applied in sequences called derivations to produce all the strings in the language of the grammar (context-free language). The information in a single derivation may be represented pictorially in a parse tree.

Examples: grammars G1 and G2.

Formal Definition of a Context-Free Grammar

Definition 2.1.

Examples of Context-Free Grammars

Examples 2.2 and 2.3.

Designing Context-Free Grammars

Four rules-of-thumb when approaching problems requiring creativity:

Union rule: divide and conquer. Make individual grammars for the simpler pieces.
DFA rule: if it's a regular expression, convert the DFA to a CFG.
Linked substring rule: use a production of the form R --> uRv.
Recursion rule: use recursive forms where necessary.

Example: Give a context-free grammar for the following language in the alphabet {a, b}:

{w | w ends in "a" or "ab"}

The language is regular, so we construct a DFA and convert it to a CFG (rule 2):

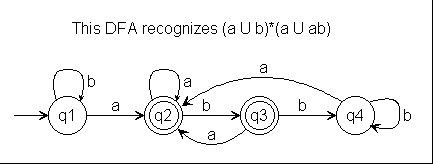
A DFA to recognize the specified language.

Then we create a rule for each transition in the DFA:

R1 --> aR2 | bR1
R2 --> aR2 | bR3 | e
R3 --> aR2 | bR4 | e
R4 --> aR2 | bR4

Ambiguity

A string could have more than one "meaning" if it has more than one parse tree. The string is derived ambiguously in that grammar.

Definition 2.4.

Some languages are inherently ambiguous.

Chomsky Normal Form

Noam Chomsky (MIT) showed that every CFG could be converted to a form in which every rule is in a form in which the right hand side consists only of binary variables or terminals. This form is useful for giving algorithms for working with CFGs.

Example 2.7.

Email: Richard dot J dot Wagner at gmail dot com