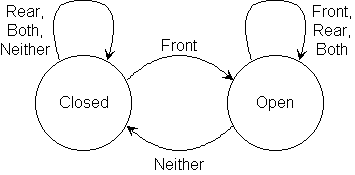
State diagram for the swinging door controller.

This is a one-way door. People enter from the front.
| input signal
| Neither Front Rear Both
------------|---------------------------------------
Closed | Closed Open Closed Closed
Open | Closed Open Open Open

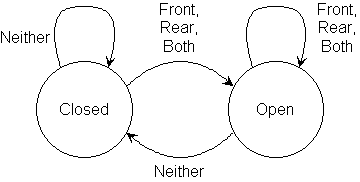
Sliding Door Opener:
This is a two-way door. People can enter and exit.
| input signal
| Neither Front Rear Both
------------|---------------------------------------
Closed | Closed Open Open Open
Open | Closed Open Open Open
A finite automaton can be represented by a state diagram that has a set of states, one a start state (input arrow), and zero, one, or several accept (final) states. Transitions from one state to another are represented by directed edges. The input is a string, and the output is either accept or reject.
The transition function, delta, is described by a table:
| 0 1
--------|-----------
q1 | q1 q2
q2 | q3 q2
q3 | q2 q2
Although not necessary, a finite automaton might have a graphical representation:
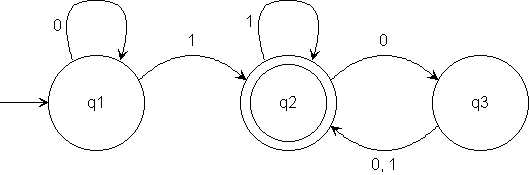
The graphical representation can help us visualize how the machine "moves" on its input.
Let A be the set of all strings that machine M accepts. Then A is the language of the machine M: L(M) = A. M recognizes A, or M accepts A. The term "recognize" is preferred to avoid confusion with the acceptance of a string by M. A machine (usually) accepts many strings, but recognizes only one language. What language does a machine recognize if it accepts no strings?
L(M1) = A = {w| w contains at least one 1 and an even number of 0s follow the last 1}
or M1 recognizes A.
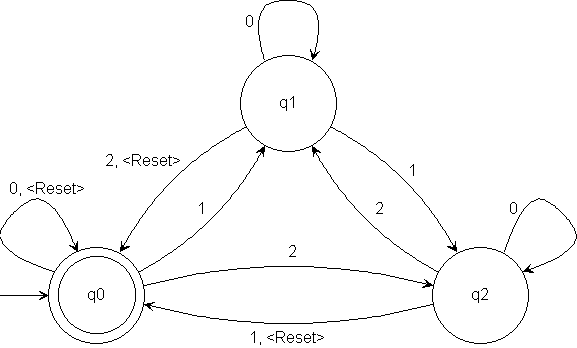
M5 accepts strings over {0, 1, 2, <Reset>} that sum to 0 modulo 3 or strings ending in <Reset>.
This definition says (informally) that there exists a sequence of states such that the input will cause a series of transitions through those states ending in an accept state.
M recongizes A if A = {w| M accepts w}. A language is regular if some finite automaton recognizes it.
Theorems:
 Email: Richard dot J dot Wagner at gmail dot com
Email: Richard dot J dot Wagner at gmail dot com
notes01a.htm, this hand crafted HTML file created August 31, 1998.
Last updated May 14, 2011, by
Rick Wagner. Copyright © 1998-2011, all rights reserved.