Holonomic Drive Analysis
This page addresses one of the issues associated with traction control for our 2009 Orange Force robot semi-holonomic drive.Case One: Rear Wheels Static
In this case, the two non-slipping front wheels are pulling the robot forward at a constant velocity V, as shown below in Figure 1:
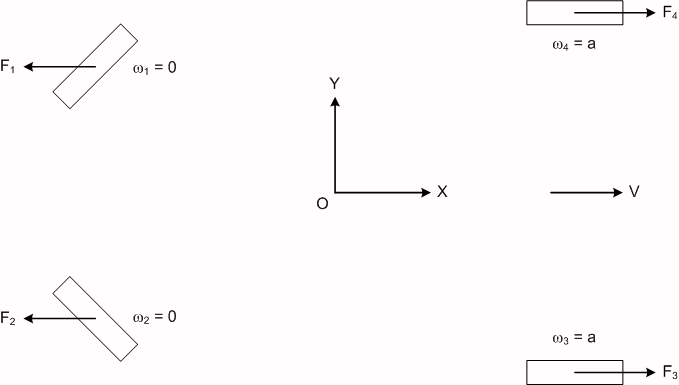
Figure 1: The robot is moving in the X direction at a constant velocity V.
In Figure 1, the two front wheels (3 and 4) are pulling the robot forward with a constant torque (realized as forces 3 and 4), while the rear wheels are not turning (omega = zero), creating drag forces F1 and F2. The forces are not balanced because the coefficient of static friction (front wheels) is greater than the cofficient of dynamic (sliding) friction (rear wheels), so the robot accelerates slightly.
Case Two: Rear Wheels Also Rotating
Now take the case where the rear wheels turn at the same angular rate as the front wheels. We can analyze this case by using a velocity vector diagram, shown below in Figure 2:
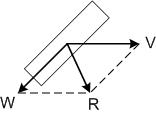
Figure 2: The rear wheels are turning at the same rate as the front wheels.
The resultant velocity vector R is the vector sum of the robot velocity (V) and the wheel tread velocity (W) due to the anglular velocity of the wheel. In this case, the magnitude of R is less than the magnitude of either V or W. The wheel force resultant is in the opposite direction of the wheel motion resultant, as shown below in figure 3:
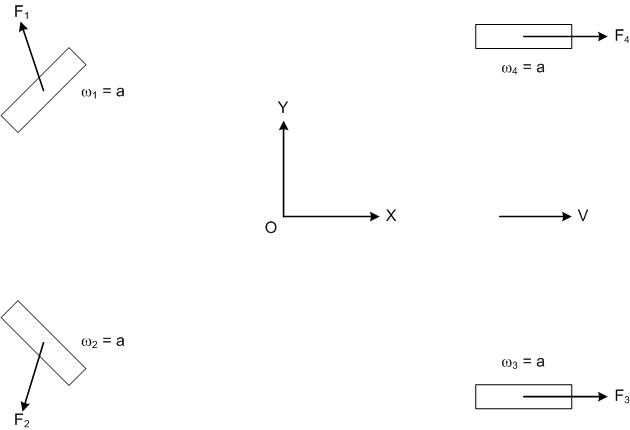
Figure 3: The rear wheels are turning at the same rate as the front wheels.
In Figure 3, the rear wheels now turn at the same speed as the front wheels which are still tracking true (not slipping). The magnitude of the force vectors has not changed, but the direction of the rear wheel force vectors has improved somewhat.
Case Three: Rear Wheels Really Spinning
Now consider the case of attempting to maximize acceleration, as shown below in Figure 4:
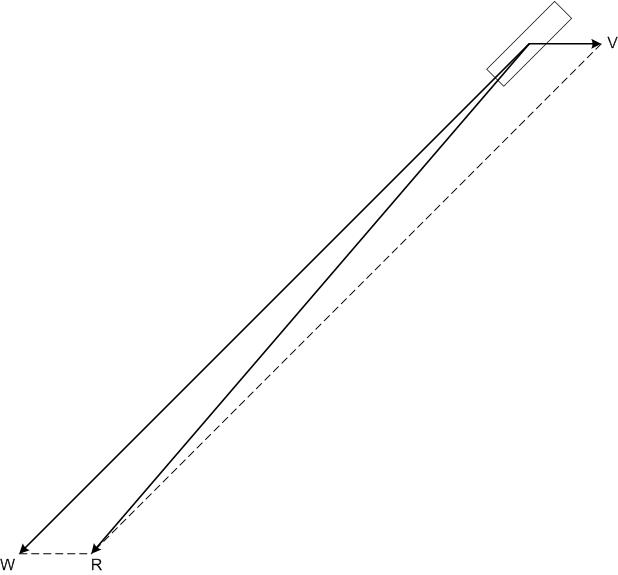
Figure 4: The rear wheels are turning much faster (10 times) than the front wheels.
The vector sum is dominated now by the wheel speed. This causes an improvement in the direction of the resultant, R, with a corresponding change in the direction of the force vector, as shown below in figure 5:
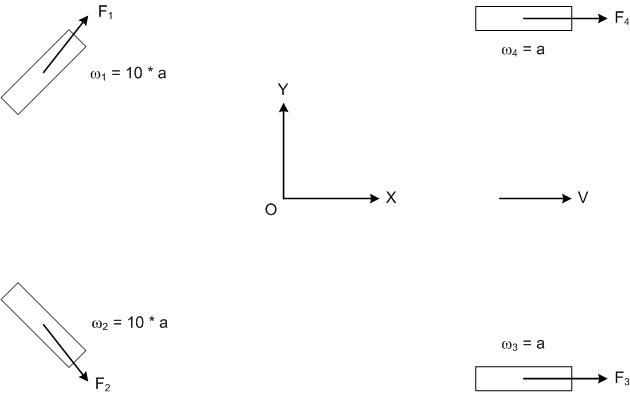
Figure 5: The rear wheels are turning much faster (10 times) than the front wheels.
The magnitude of the force vectors is still the same for the rapidly spinning rear wheel case, but the direction is approaching the wheel motion direction. No matter how fast the rear wheels turn, the direction of the force vector at the rear wheels can never exceed 45 degrees (the angle of orientation of the rear wheels).
Notice that this analysis requires knowledge of the state vector (V). If it can be known that the front wheels are not slipping, then V (and also theata, the robot rotation rate about its vertical axis) can be computed from the front wheel rates.
BCR Supplemental Page
Holonomic.html, this hand crafted HTML file created February 18, 2009.
Last updated February 19, 2009, by Rick Wagner.