High Velocity Liquid Droplet Gun as a Weapon for Space Warfare

November 17, 2006

1. Abstract

A novel space weapon system is discussed, with feasibility, prior art, and variations. High speed liquid (e.g., water) droplets can damage or destroy space systems. Droplets missing their targets will subsequently evaporate and not endanger friendly space vehicles in the future.

2. Introduction

Various kinetic energy and directed energy weapons systems have been proposed for space use. With the recent Presidential signing of the new space policy document [1] on August 31, 2006, cost-efficient weapons for space, both offensive and defensive, become more important. A standoff weapon is one that can be used from a considerable distance, one that allows attack or defense while minimizing exposure to hostile fire. A gun that can fire high velocity liquid bullets can be used destroy or seriously degrade enemy spacecraft from very great distances if the aiming accuracy and dispersal pattern can be sufficiently controlled. Using very small liquid droplets allows a very high number of projectiles to be used, and against spacecraft in different orbits from the gun platform, can have very high impact energies due to the difference in orbital velocities of the spacecraft.

Conventional metallic bullets or shot, no matter how small they might be, if they should miss their target, will remain in orbit and pose a hazard to friendly spacecraft. A suitable liquid, such as water, on the other hand, will vaporize in vacuum over time. Another advantage of using liquid projectiles is that the quantity, velocity, and size of droplets can be varied depending on the attack parameters desired. At closer ranges, larger drops in a narrow dispersion pattern will be required. At longer ranges, a larger number of smaller droplets may be more effective.

3. Liquid Droplet Gun Description

Industrial water jets are used for cleaning surfaces, de-burring, and cutting metals and other materials. A typical ultra-high pressure industrial water jet will operate at 40,000 psi and deliver about ten gallons per minute (10 gpm) in a continuous stream of water 0.050 inch in diameter at a speed approaching 1,000 feet per second (fps). While such an industrial system could certainly do damage to an enemy spacecraft, much more efficient systems are possible. We can construct an efficient space water gun along the lines of a conventional sporting air rifle. A straight smooth barrel to guide the accelerating water droplet is connected to valved reservoirs of liquid projectile material and compressed gas. Such a gun might look something like that shown below in Figure 1:

Figure 1: Compressed gas liquid drop gun schematic diagram. The liquid valve is electrically
controlled. The compressed gas valve is fast acting and electrically controlled for rapid pulse
firing.

A small amount (one drop) of water (for instance) is let into the gun tube. Then, the compressed gas (helium, for example) valve is opened and the water drop accelerates down the tube and exits at the muzzle end. We can compute the muzzle velocity, V, for the water drop, as shown. We assume, for purposes of illustration, that the gun tube is one foot long and one half of an inch (0.042 ft.) in diameter. The density of water is 62 lb_m/ft³. If we let just enough water in to the gun tube to make a spherical drop that has the same diameter as the tube (due to possible wetting adhesion properties of the tube interior, the drop will perhaps assume a cylindrical shape while in the tube (in zero gravity), and will assume a spherical shape when free flying. Larger amounts of water will lead to clusters of multiple drops being fired, with muzzle velocity reduced from that of the lighter single drops), the water drop mass will be 7.47 x 10^-4 lb_m = 2.32 x 10^-5 slug.

The area of the gun bore is 1.38 x 10^-3 ft², and the pressure of the gas in psf is 5.76 x 10⁶. The force applied to the drop from the gas will be 7,976 lb_f. Acceleration of the drop will be 3.43 x 10⁸ ft/s². With constant acceleration (which it will be if the gas reservoir is sufficiently large), the formula for velocity is

V² = 2 * a * d (equation 1)

Where a is the acceleration of the water drop and d is the distance the drop travels down the gun barrel. [2] Solving equation 1 for V gives

V = 2.62 x 10⁴ ft/s (equation 2)

Such a velocity represents a significant orbital change. Hence, standoff distances are feasible. Higher velocities (for a given propellant gas pressure) can be achieved by using smaller diameter liquid drops or longer gun barrels.

For a 0.5 inch diameter water drop at 26,200 ft/s velocity, the kinetic energy will be 7,960 ft-lb. Such energies are capable of severely damaging spacecraft structures and sensors. Higher energies per droplet can be obtained when closing velocity or orbital velocity differences are taken into account.

It should be noted that with distant targets, evaporation will cool the droplet until it freezes solid. However, the energy of liquification is small compared to the kinetic energy, so whether the droplet is solid or liquid will make little difference in its damage potential on enemy spacecraft. [3] The frozen droplet will eventually evaporate (sublime) completely, leaving no hazard for friendly space vehicles. The duration of projectile droplets will depend on size, material, and the amount of exposure to sunlight. Other suitable materials besides water might include glycols, butanol (butyl alcohol), pentane, and other alcohols and hydrocarbons. Exothermic materials such as hydrazine will add heat of decomposition to the impact kinetic energy.

A concept sketch of a space weapon system is shown below in Figure 2:

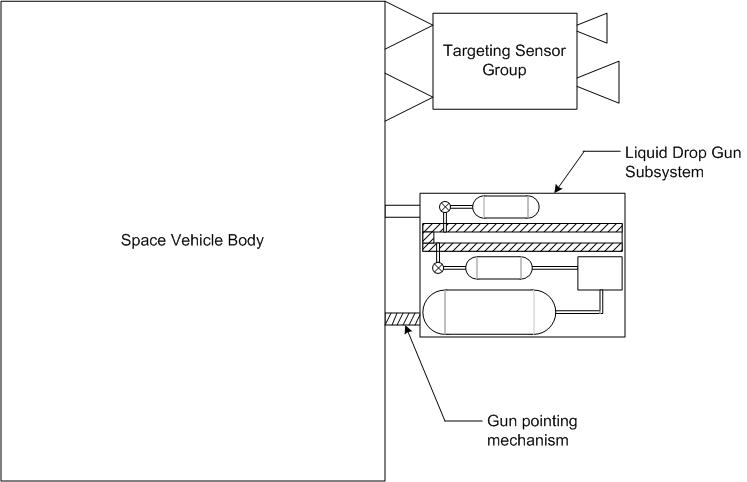
Figure 2: Liquid drop projectile space weapon system concept sketch.

A space weapon system utilizing the liquid drop gun would need to acquire targets using a suitable sensor system such that the orbital state vector parameters can be established with sufficient precision to compute a feasible intercept trajectory for the liquid drop projectiles. An onboard weapon fire control system will compute optimal liquid injection volume, gas pressure or volume (as controlled by the rapid valve), projectile firing pulse rate, number of pulses, and aim direction. It is possible to use spacecraft body pointing for aiming the gun, but higher battle agility may be achieved by a gun pointing mechanism as shown. Keeping the gun bore centerline near the space vehicle center of gravity will minimize any slewing tendency due to gun reaction force. For aiming and controlling the weapon, an algorithm will need to take sublimation rate of the projectiles and solar photon pressure on the projectiles into account. The physics of such computations is well known and rather straight-forward.

4. Prior Art

Water jet cleaning and cutting equipment is available for industrial use, and while industry literature addresses safety hazards of this equipment, weapon use is not addressed. Truck-based water cannons were used in the 1960s for riot control. Related space weapons include smart rocks (small rockets used as kinetic kill vehicles), brilliant pebbles (a more sophisticated version of smart rocks), and a space shotgun (a large gun tube using liquid propellant shooting spinning packages of solid shot, e.g., lead pellets).

5. Variations on the Concept

Electrostatic acceleration of liquid projectiles is probably feasible and may lead to even higher energy efficiency or projectile velocity.

6. Strategic Considerations

Once an enemy spacecraft is targeted and fired upon, at space operations distances, considerable time can pass until the projectiles impact the target. Needless to say, the weapon system can then acquire and fire upon additional targets. Any space vehicle targeted will have time to accelerate in an attempt to avoid the projectile stream. This kind of defense will be extremely difficult to implement as the pneumatic gun described here will produce almost no signature when fired, and the projectiles, being a dialectric material (e.g., water), will not be detectable by radar, no matter how short the wavelength. Visual acquisition of small water droplets at significant distances will also be extremely difficult. One defensive strategy is simply to make random delta-V maneuvers when within range of an enemy gun platform, but that will cause the defender to expend valuable maneuvering fuel. Therefore, the system should have the capability of revisiting targets to detect evasive action and re-attack if necessary.

7. References

[1] George W. Bush, U.S. National Space Policy, the White House Office of Science and Technology, August 31, 2006.
[2] David Halliday and Robert Resnick, Fundamentals of Physics, John Wiley & Sons, Inc., 1974.
[3] Mythbusters, Episode 9: Chicken Gun, http://kwc.org/mythbusters/2004/02/mythbusters_chicken_gun.html

Richard dot J dot Wagner at gmail dot com