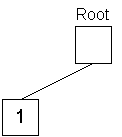
The first (leftmost) digit of 1997 is stored in the tree.
A tree data structure and associated algorithms have been created that provide the following functionality and performance properties:
| Function | Time Complexity (allows duplicate keys) |
Time Complexity (no duplicate keys) |
Comment | |
|---|---|---|---|---|
| 1 | Insert an object with a key string into a container. |
O(1) | O(log n) | n is the number of objects stored in the container. |
| 2 | Determine whether an object is in a container based on some key string for the object. |
O(1) | O(log n) | |
| 3 | Retrieve an object from a container based on some key string. |
O(1) | O(log n) | |
| 4 | Determine how many of an object with the same key exist in a container. |
O(1) | Does not apply if duplicate keys are not allowed. | |
| 5 | Write the objects from a container into an array in sorted order based on their keys. |
O(n) | O(n log n) | |
The storage space required for the objects is O(n). Combining the above functions 1 and 5 gives an O(n) sort algorithm for objects with bounded-length keys (e.g. people sorted by social security number). This algorithm has been implemented and tested, with test results corroborating the O(n) complexity from analysis.
The better-performing duplicates-allowed functions may be used with fixed field key relational databases if some external mechanism is used to preclude duplicate keys (such as using serial numbers for keys as is a common practice in many implementations).
Many practical applications have a fixed key length, such as the 9-digit social security number (SSN), name string (last + first + middle), or other property of the stored object. If, as in a relational database, duplicate keys are not allowed, the fixed key length puts an upper limit on storage capacity that is not usually reached in practice.
In such practical applications, a string tree as described here can provide keyed storage of data objects with the depth of the tree equal to the length of the largest key. This constant bound on the depth of the tree allows the implementation of a linear sort function, as described and demonstrated below. Moreover, the sort algorithms described here are stable, that is, they preserve the initial order of items with equal keys [5].
Other known O(n) sorting algorithms such as counting sort, radix sort, and bucket sort [2], impose restrictions on the sorted objects. For example, bucket sort requires both that the numbers to be sorted to be within a predetermined range and that there be no duplicates [1]. The O(n) sort described here imposes no such restrictions. However, as n grows without bound, duplicates will be encountered when the key word length is less than log n.
First, a StringTreeNode object is created with a null key character and null object queue to serve as the tree root. Then, the first digit (left end) of the first object's key is read and a new StringTreeNode is created with that digit being used for the key character. The new node pointer is stored in the root's array of children indexed by key character. The resulting structure is shown below in figure 1:

Then the process is repeated for the the next three digits of 1997:
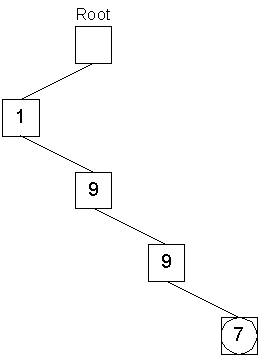
Storing the object with key 1997 took four operations to create key nodes and one operation to push the object onto the leaf node queue. Similarly, the object with key 1999 is stored:
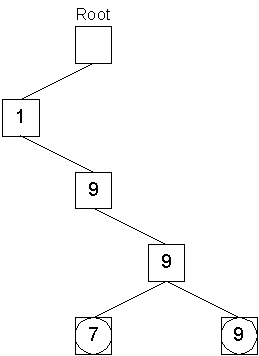
Storing the object with key 1999 took three operations to locate the node with the digit 9 at the third level of the tree, one operation to create the leaf with the digit 9, and one operation to push the object onto that node's queue. Next, the object with the key 2003 is stored:
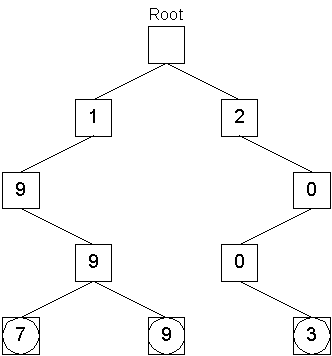
Finally, the objects with keys 2011 and 2017 are stored in a similar manner:
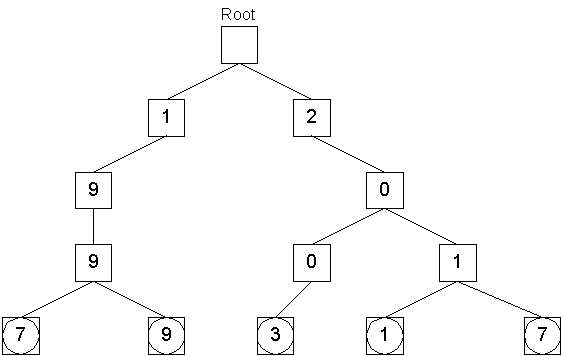
All these insert operations have a time complexity on the order of the depth of the tree, which is the number of digits or characters in the key. For bounded-length keys, the insert operation is performed in constant time. For unbounded keys, such as for storing the prime numbers themselves, the depth of the tree is log n, where n is the largest number stored (the number of primes up to integer m is O(m)). The key itself can be recovered by traversing upward through the parents to the root. A parent pointer is provided in the StringTreeNode for this purpose.
Note that data objects are not necessarily stored at leaves and that the string tree data structure is not a binary tree. For example, if we wanted to add data with the keys 13, 17 and 19 to the tree we would have:
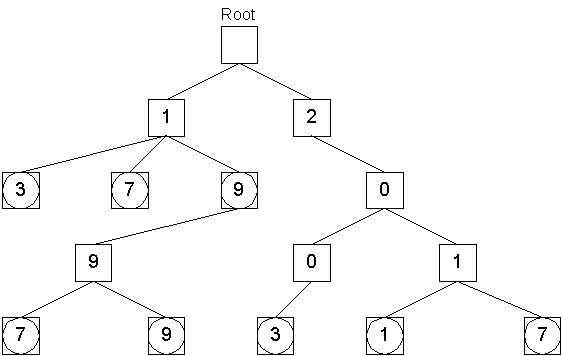
The data structure allows for storing objects with duplicate keys because each node has a queue of data objects. Objects with the same key are stored by pushing them into the queue of the same node, and are recovered by popping them off until the queue is empty.
1
10
11
101
111
and the following are the same strings in alphabetical order:
1
10
101
11
111
just as these strings are in alphabetical order:
b
ba
bab
bb
bbb
A convenient property of the string tree utility data structure is that a preorder (depth-first) traversal encounters the objects in alphabetical order of the keys, and a breadth-first traversal encounters the objects in numerical order.
The time required to visit every node in the tree is O(n) where n is the number of objects stored in the tree. This applies to both variants of the traversal function because each node of the tree is visited. This holds for trees where data objects are stored only in leaves because the number of internal nodes for any tree with a bounded branching factor (which is a property of the string tree) is a constant function of the number of leaves in the tree [4]. For string trees with unbounded depth (as in the case of unbounded key length (which must hold for the no-duplicates case)), the traversal time is O(n log n).
Functions were written to create arrays of person pointers and rock pointers. The people were created by hard coding data. Rocks were created by assigning colors at random with sequencial keys. The rocks were then permuted randomly in the array to test the sorting functions.
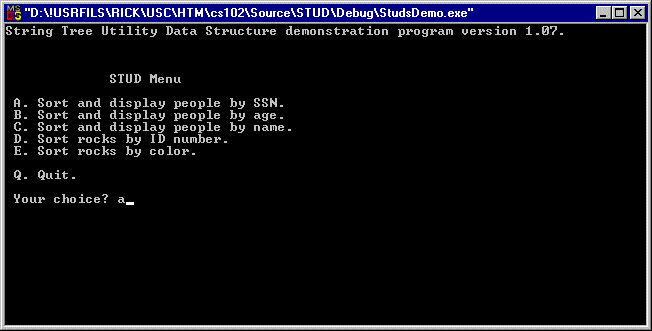
A console menu user interface was created for testing as shown below in figure 7:
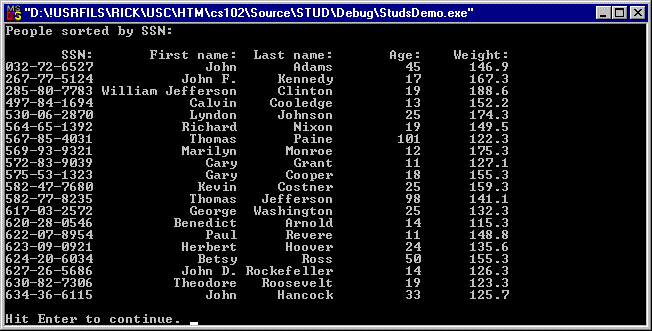
For option A, people's SSNs are not duplicated. Each node in the tree will have at most one data object stored in its queue. Figure 8 shows the output from option A:
The people's ages are duplicated in some cases. Some nodes will have several person objects stored in their queues. Figure 9 shows the output from option B:
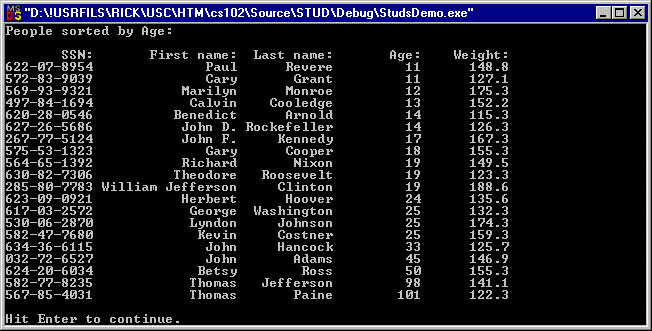
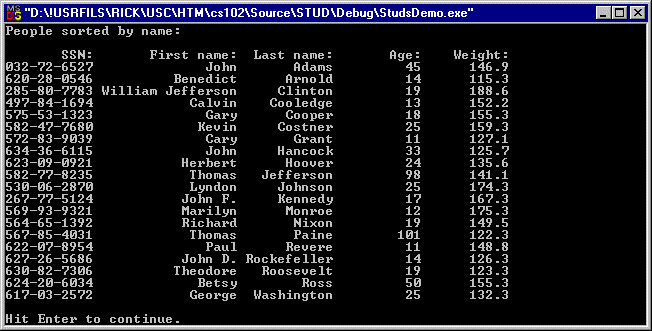
People's names include spaces and punctuation. The last and first names are concatenated before sorting and the output of option C is shown in figure 10:
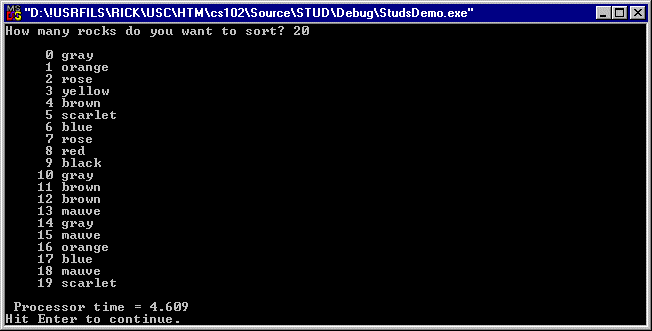
Option D sorts rocks by sequential ID number (no duplicates) and its output is shown in figure 11:
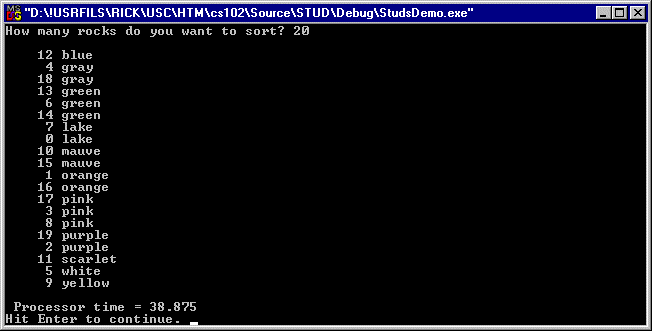
Option E sorts rocks by color (lots of duplicates) and its output is shown in figure 12:
Here is the function to sort the rocks by color:
// Sort rocks by color:
void rocksByColor(int iNumRocks)
{
int i = 0; // Loop index.
int iManual = 0; // Flag for manual entry.
Rock** array; // Array of rock pointers.
StringTreeNode<Rock>* rockRoot = NULL; // Root of the tree of rocks.
double dfProc = 0; // Statistical information variable.
if (iNumRocks == 0) // Get the number from the user.
{
iManual = 1;
cout << endl;
cout << "Sort rocks by color:" << endl << endl;
cout << "How many rocks do you want to sort? ";
cin >> iNumRocks;
}
array = new Rock*[iNumRocks]; // Create the array of pointers.
buildRocks(array, iNumRocks); // Create rocks randomly.
rockRoot = new StringTreeNode<Rock>('.'); // The root of the tree.
for (i = 0; i < iNumRocks; i++) // Insert the rocks into the tree.
{
rockRoot->addObject(array[i]->getColor(), array[i]);
}
i = 0;
rockRoot->preOrderStoreObjects(array, i); // Traverse the tree in preorder
// and store the rocks back in the
dfProc = ((double) clock()) / CLOCKS_PER_SEC; // 1000 clocks per second.
if (iManual)
{
cout << endl;
for (i = 0; i < iNumRocks; i++)
{
array[i]->print();
}
}
else
{
cout << endl << " Processor time = " << dfProc << endl;
}
}
Notice that the sorting is accomplished by first inserting all the rocks
into a new tree (time order n) and then preorder traversing the tree and
storing the rocks in the array (time order n). This code illustrates
that the STUD is easy to use for a sorting application. The complete C++ source code is available
on condition that copyright and patent information are retained in the source and that attribution
is given for any usage, along with this condition for any further distribution:
StringTreeUtility.h
StringTreeUtility.cpp
StudsDemo.cpp
The resulting program output looked like this:
Tests were performed for rocks sorted by ID and by color. Raw data for the ID sort runs are shown here:
String Tree Utility Datastructure Performance Tests 24-Mar-00 Rocks sorted by unique numerical ID (no duplicates) Number Avg. Time Time Time 1000 0.062 0.063 0.062 0.062 2000 0.130 0.141 0.125 0.125 3000 0.1875 0.187 0.188 4000 0.2575 0.265 0.25 5000 0.335 0.328 0.334 0.343 6000 0.4065 0.407 0.406 7000 0.484 0.484 0.484 8000 0.5545 0.562 0.547 9000 0.64 0.64 0.64 10000 0.7425 0.75 0.735 11000 0.844 0.844 0.844 12000 0.974 0.984 0.969 0.969At least two runs were performed for each number of rocks. When graphed, the average data look like this:
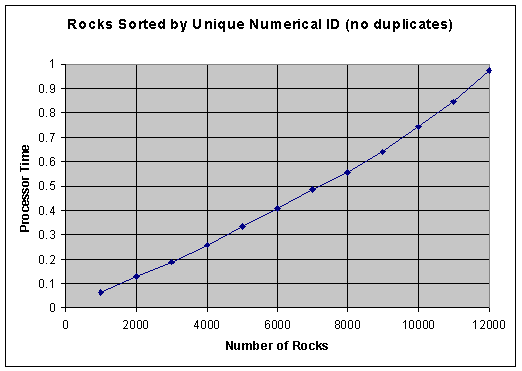
Notice the slight upward curve due to the O(n log n) performance predicted for this algorithm. Based on the difference in time from 1000 rocks to 2000 rocks, O(n log n) predicts a time of 0.96 seconds for 12000 rocks, within one percent agreement with the measured 0.97.
When graphed, the data for sorting rocks by color (many duplicates because there are only 16 colors) look like this:
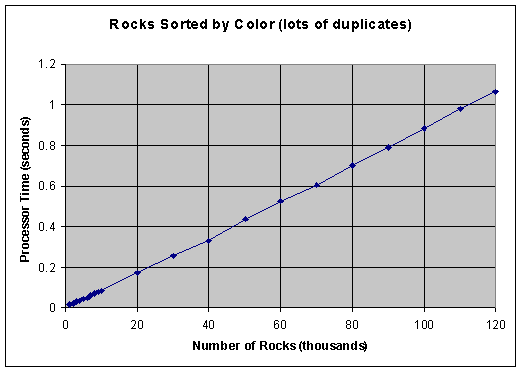
Notice that this indicates a linear sort, as analysis predicts.
Source code is available for educational purposes: StudTest.java is the main file. StringTreeNode.java, ListNode.java, Queue.java, and Person.java are necessary object files.
As will be noticed, StudSort is significantly faster with more than 5000 people. Some Java runtime systems will have memory shortages above a few hundred thousand people. Such problems are mitigated by programming in C++. Note also that results with larger numbers of people will be erratic due to the virtual memory paging in many systems. The implementation of QuickSort used here is adapted from Structured C for Engineering and Technology, third edition, by Adamson et al. [1] (page 403), and uses more memory than StudSort.
[2] Thomas H. Cormen, Charles E. Leiserson, and Ronald L. Rivest, Introduction to Algorithms, The MIT Press, 1990.
[3] Stefan Nilsson, "The Fastest Sorting Algorithm?," Dr. Dobb's Journal, April 2000.
[4] Kenneth H. Rosen, Discrete Mathematics and Its Applications, Fourth Edition, McGraw-Hill, 1999.
[5] Robert Sedgewick, Algorithms, Second Edition, Addison-Wesley, 1988.
Copyright 2000-2019 by Rick Wagner, all rights reserved.
This page established March 25, 2000; last updated by
Rick Wagner,
November 9, 2019.
United States patent 6,741,999, awarded May 25, 2004.