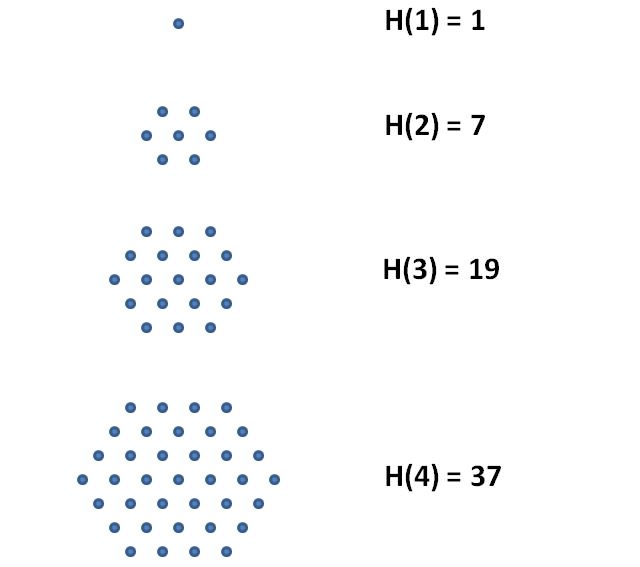
The first four hexagonal numbers.
Of particular interest are the hexagonal numbers, those that can be arranged into a hexagonal array as shown below:

Number Triangle Square Hexagon Cube Hex Pyram Mersene H Factors M Factors 1 1 1 1 1 1 3 prime prime 2 3 4 7 8 8 5 prime prime 3 6 9 19 27 27 9 prime 3, 3 4 10 16 37 64 64 17 prime prime 5 15 25 61 125 125 33 prime 3, 11 6 21 36 91 216 216 65 7, 13 5, 13 7 28 49 127 343 343 129 prime 3, 43 8 36 64 169 512 512 257 13, 13 prime 9 45 81 217 729 729 513 7, 31 3, 3, 3, 19 10 55 100 271 1000 1000 1025 prime 5, 5. 41 11 66 121 331 1331 1331 2049 prime 3, 683 12 78 144 397 1728 1728 4097 prime 17, 241 13 91 169 469 2197 2197 8193 7, 67 3, 2731 14 105 196 547 2744 2744 16385 prime 5, 29, 113 15 120 225 631 3375 3375 32769 prime 3, 3, 11, 331 16 136 256 721 4096 4096 65537 7, 103 prime 17 153 289 817 4913 4913 131073 19, 43 3, 43691 18 171 324 919 5832 5832 262145 prime 5, 13, 37, 109 19 190 361 1027 6859 6859 524289 13, 79 3, 174763 20 210 400 1141 8000 8000 1048577 7, 163 17, 61681
The formula for the triangular numbers is
The formula for the square numbers is, of course, just n2. The formula for the hexagonal numbers utilizes the formula for the triangular numbers:
A hexagonal pyramid is built by stacking incrementally smaller hexagons. It turns out that the volume of a hexagonal pyramid of size n is exactly equal to the cube of n:
The factors of the first 20 hexagonal numbers are shown in the column labeled "H Factors." As can be seen, there are more prime hexagonal numbers than rectangular ones. The trend continues through the first fifty hexagonals as shown in this Excel file.
For comparison, the first 20 Mersene numbers (of the form M(n) = 2n + 1) are shown. Their factors are shown in the column labeled "M Factors." As can be seen, the hexagonal primes appear to be more numerous than the Mersene primes.
 Email Richard dot J dot Wagner at gmail dot com
Email Richard dot J dot Wagner at gmail dot com
index.html, this hand crafted HTML file was created November 25, 2011.
Last updated July 28, 2014, by
Rick Wagner. Copyright © 2011-2014, all rights reserved.