Robotic Navigation

Robot navigation is a research topic that seeks to develop good ways for robots to find their way in the world. I developed a 2D navigation program that simulates the navigation of a polygonal robot among polygonal obstacles on an infinite plane. The "standard" visibility graph approach runs in n-squared time where n is the number of vertices in the obstacles. My simulation uses a locality heuristic which in uncluttered environments runs in time n.

You can download a copy of the program navig.zip for 16-bit Windows. You will need VBRUN300.DLL if you don't have it already. Check your Windows/system directory. vbrun.zip is a zip file containing VBRUN300.DLL.

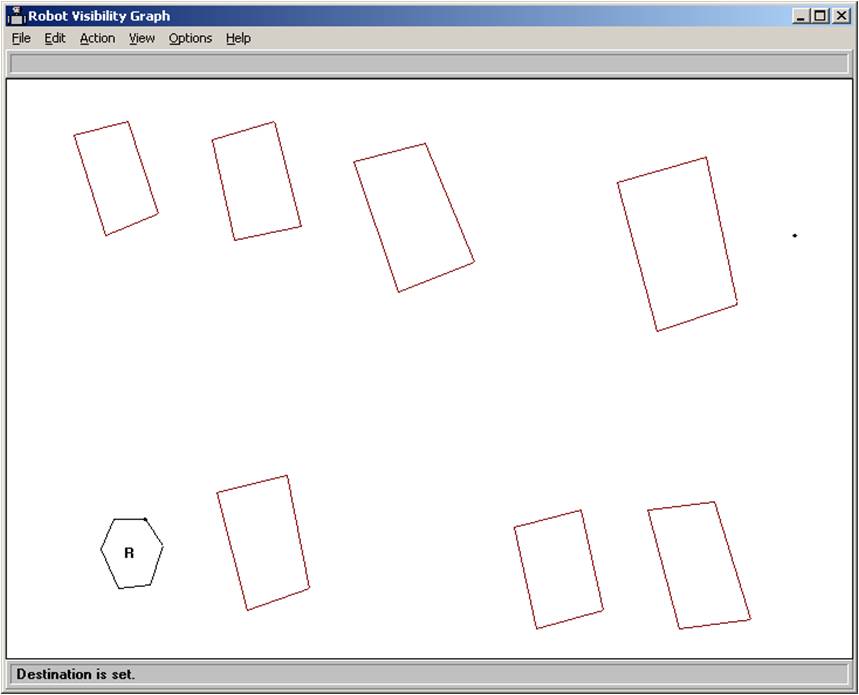
Visibility graph demonstration program. The robot is represented by the hexagon in the lower left
corner. The goal point is in the upper right corner. The red rectangular obstacles represent cars in a parking lot.

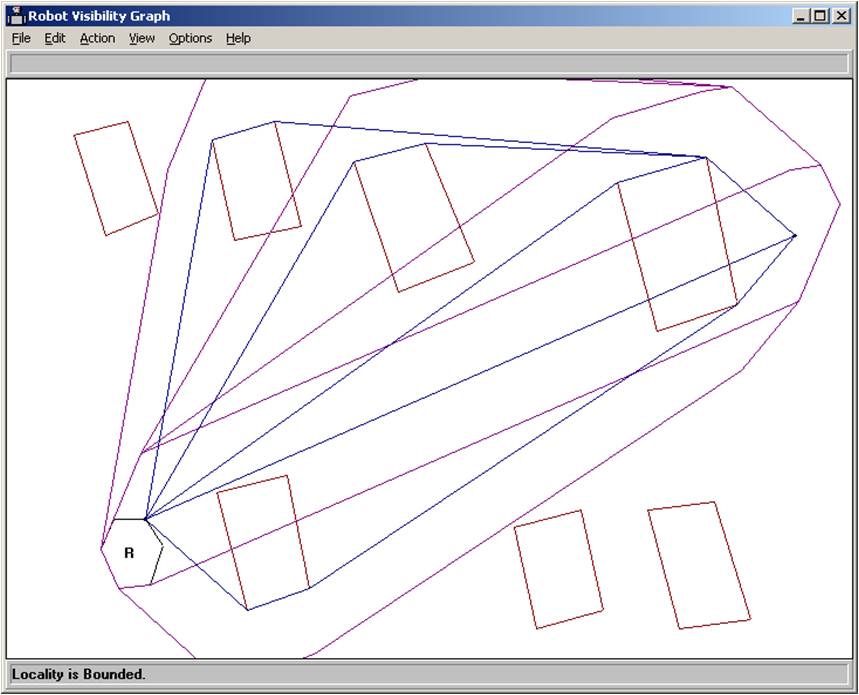
The locality is bounded by drawing a line from the robot to the goal and then “growing” this
line by the robot (Minkowski sum). If the grown line contacts any obstacles, those obstacles are
included in the locality and the process repeats until no new obstacles are included in the locality.
Here, four obstacles are included in the locality.

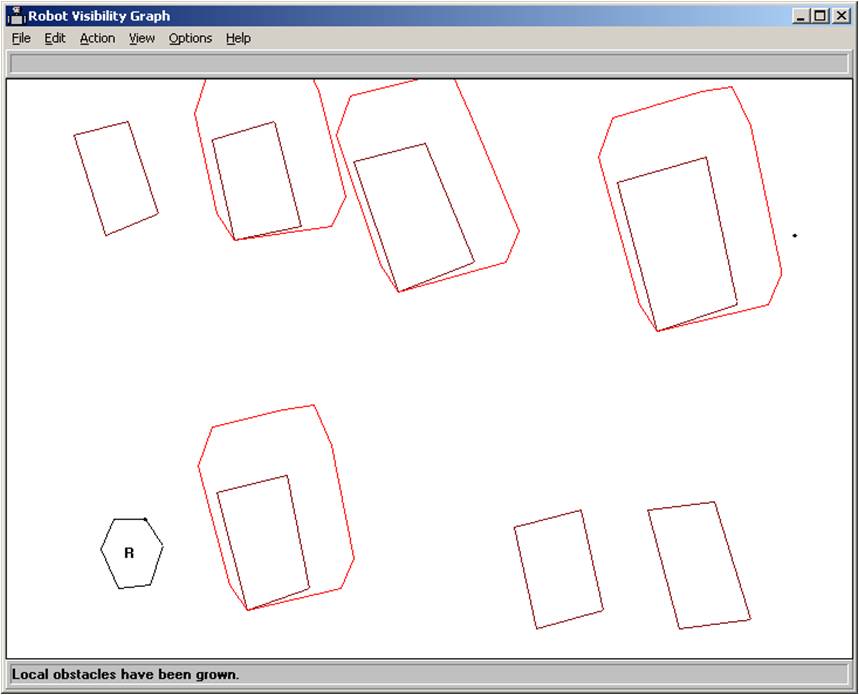
Next, the local obstacles are “grown” by the robot (take the Minkowski sum).

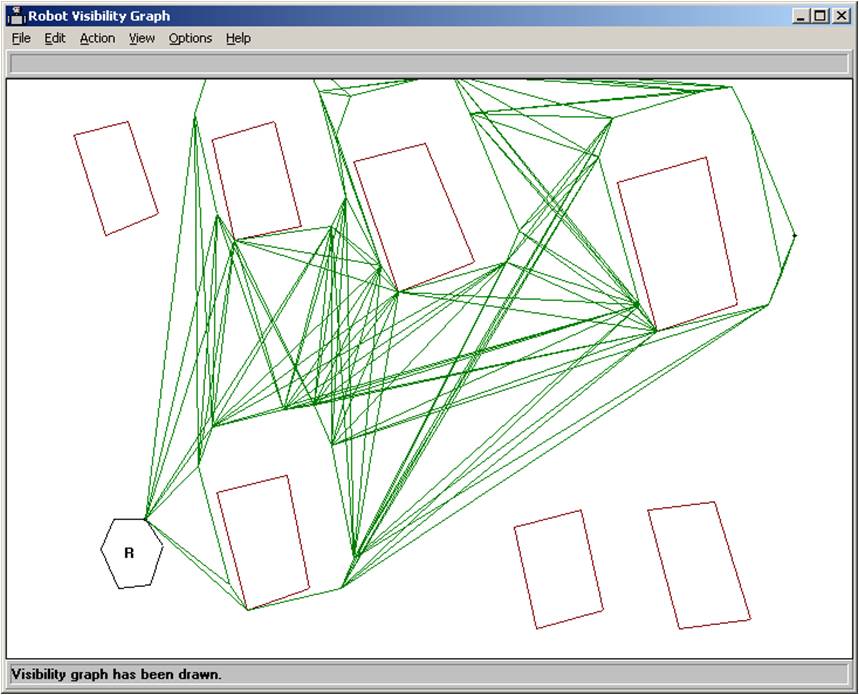
Then we draw the visibility graph of the robot, grown local obstacles, and the goal point.

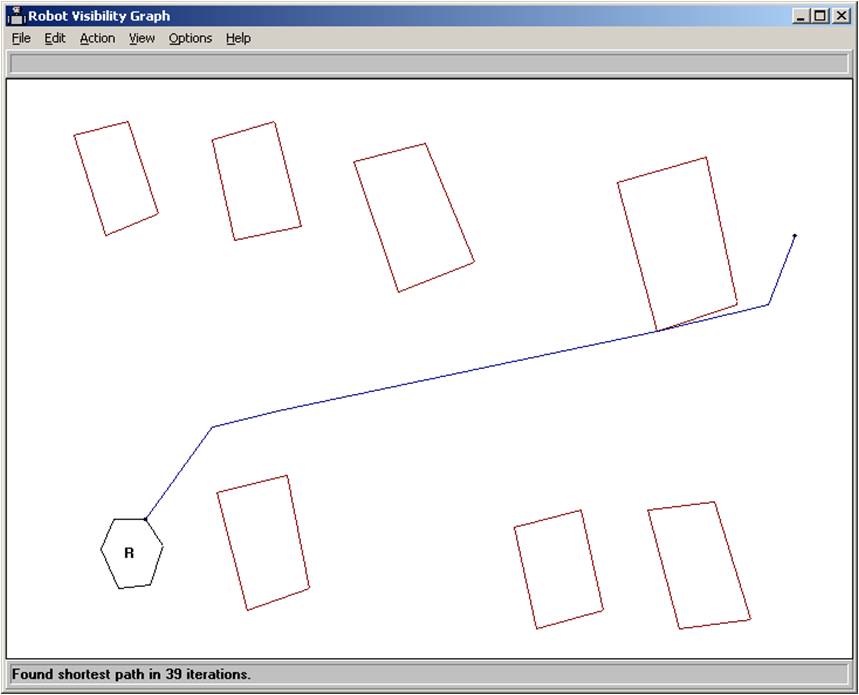
The shortest path in the visibility graph is then found using Djikstra’s algorithm.

The intuition behind this locality heuristic is that if you could pull a string tight between the goal points and it didn't touch any obstacles, you could just go straight to the goal if the robot is very small. If you use a fat string, then a fat robot could go straight to the goal. In uncluttered environments, that will often be the case. As clutter increases, the string might touch some obstacles, but going outward from the initial straight try will likely find a path nearby. Nearby paths will generally be shorter than further away ones.

USC home page.

Email Richard dot J dot Wagner at gmail dot com