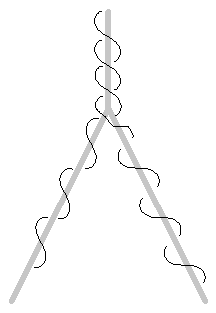
Figure 1: Binary branch wired with direct method.
Using either annealed copper or aluminum wire to modify and hold the shape of a tree allows the bonsaist to realize the plastic aspect of his art. Cutting and carving constitute the subtractive aspect, while only nature can perform additive operations on bonsai. Other techniques for shaping trees may also be used either separately or in conjunction with wiring. These techniques include tying branches down with string, hanging weights on branches, and the use of various levers or jacks. Wiring provides a general technique for achieving effective branch placement and so is one of the most commonly used techniques.
To perform this technique, a piece of wire of the appropriate size (diameter) and length is wound around the trunk/branch system. The winding with wire adds both plasticity and stiffness to the system. The wire is left in place for several months while new growth forms to make permanent the shape change induced by the wiring.
The proof is by induction, first, over the branching factor of the tree, and second, over the branches of the tree. I shall show that there are always multiple solutions to the wiring problem.
Bonsai generally have fairly low branching factors, but the following proof is general and applies to any tree. First we take the case of the simplest branching (binary, branching factor of two) as shown below in Figure 1:

The direct approach of Figure 1 starts at the root side of the branch and winds the wire around one of the branches. Then it starts again at the root side and winds the wire around the other branch. In this way, a large number of branches could be wired, but the root side of the branch would have an unlimited number of wires on it, and for practical considerations, we wish to limit the number of wires on any branch. Therefore, we use the indirect method of Figure 2:
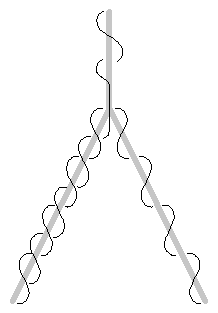
We establish the basis step of the induction with the indirect wiring of Figure 2: wire the two leaf side branches first with one piece of wire and then go back and wire the root-side branch and continue through one of the leaf side branches (the left one in this case).
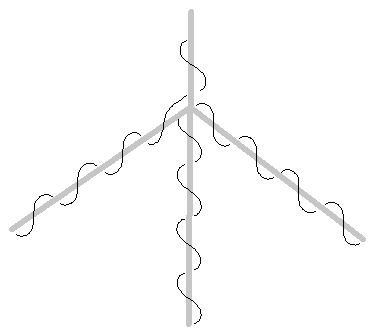
Next, we show by induction on the number of branches that we can have an unlimited number of branches without any crossed wires. Figure 3 shows the result for three branches. In the odd number branchings there are no doubled wires.
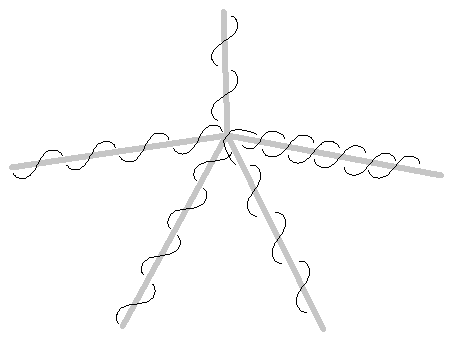
Figure 4 shows a configuration for four branches. It should be noted in the place at the crotch where it appears the wires cross that they are actually passing on different sides of the crotch (one in back, the other in front). Notice that there are multiple solutions possible (the double wired branch could be any of them). This illustrates, by induction, the general technique: any number of branches at a single branching can be wired without crossing. Now we extend the branch result to the entire tree by induction. Observe that every leaf-side branch can have any number of branches itself. Those sub-branches of any branch are handled similarly to the branch itself. This completes the proof. In addition to the multiple solutions noted above, the total number of solutions is doubled with allowing left-right winding symmetry. Therefore the number of fully wired configurations is at least two times the minimal branching factor.
 Email Richard dot J dot Wagner at gmail dot com
Email Richard dot J dot Wagner at gmail dot com
index.html, this hand crafted HTML file created June 27, 2000.
Last updated March 13, 2019, by
Rick Wagner. Copyright © 2000-2019, all rights reserved.